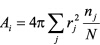NSOL

A numerical calculation program of molecular surface area, volume, and solvation energy

Masato Masuya
Computing and Communications Center, Kagoshima University
masatom@biocomputing.cc

Introduction

In computer simulation of proteins and nucleic acids, such as MD and/or MC, conformational energy + solvation energy calculation is needed. However, solvation energy calculation (implicit water, PB, RISM, etc.) is very time consuming. Therefore it can be applied to small system, or it can be included as implicit solvation effects, such as continuum model using distance dependent dielectric constant. While, there exist two methods that calculate solvation energy using solvent accessible surface area; ASP (atomic solvation parameters) model and GB/SA. In these methods, as solvent accessible surface area calculate fast, solvation energy could be calculate fast. So I decided to develop fast algorithm for molecular surface area calculation. NSOL is a fast solvation energy calculation program using fast molecular surface area calculation algorithm.

Definition of Solvent Accessible Surface Area

Solvent accessible surface is that part of the surface of a sphere centered at an atom with r_vdW + r_sol, where the center of a spherical solvent molecule can be placed in contact with the atomic van der Waals sphere (r_vdW) without penetrating other atoms. Solvent accessible radius is defined as van der Waals radius + average radius of water molecule, usually 1.4 angstrom. Because of geometrical difficulty and finite accuracy of a computer, solvent accessible surface area has been calculated approximately. There are two method of calculation: an approximate analytical method and a finite accuracy numerical method.

^*Bondi, J.Phys.Chem., 68, 441, 1964.

Analytical vs. Numerical Method

Analytical:

• Complex
  Two spheres case, three spheres case, four or more spheres cases are exist.
• Singularity
  In very near case, surface area cannot be calculated.
• Approximation
  To avoid singularity, several approximation algorithms have been developed.
• Easy derivative
  First and second derivatives can be defined mathematically, but approximately.

Numerical:

• Simple
  Not depends on spatial position of spheres.
• Stable
  Singularity problem never occurs.
• Accurate
  Depends on point distribution method and numbers of points. But accurate results can obtain at many points case.
• Numerical derivative
  Time consuming and error accumulation.

Because of its stability, I adapt a numerical method.

Numerical Surface Area Calculation

Surface area of atom group i is obtained by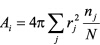
,
where r_j: solvent accessible radius (van der Waals radius + 1.4) of atom j,
n_j: number of points on atom j not occluded by other atoms,
N: number of distributed points on an atom.

Points Distribution

It is permitted up to 12 points for distributing points equally. Several methods have proposed so far:

• Tetrahedral tessellation
• Triangular tessellation
• Icosahedral tessellation
  Eisenharber et al.(Journal of Computational Chemistry, vol.16, p.273, 1995)
• Lattice tessellation
  Shrake and Rupley(Journal of Molecular Biology, vol.79, p.351, 1973)
• Latitude / longitude tessellation
• Minimum energy
  Bliznyuk and Gready(Journal of Computational Chemistry,vol.17, p.962, 1996)

Saff's(The Mathematical Intelligencer, vol.19, p.5, 1997) distribution by energy minimization gives the best results.

Neighbor List Reduction

To accelerate the computation, selected neighbors of a central atom to be removed from the computation preprocessing step. Such as;

• DCLM (Eisenharber et al.)
• NLR, BAE (Weiser et al.)

NSOL 1.x adopt a method that uses artificial grid as the same as Eisenharber et al. This is a standard approach in computational geometry to group spatially close objects. In difference of NSC, an implementation of DCLM, NSOL 1.x has an optimized code for vector processor.

1. Determination of the minimum and the maximum of the x-,y-,z-coordinates of all atoms.
2. Make large box that contains all atoms.
3. Divide large box by small cube that edge length is 2 x r_max.
   Each atom has neighbors only in its own cube and in its neighboring cubes.
4. After making neighbor list, overlap checking is executed to each distributed points.

The DCLM method of Eisenharber et al. uses the second cube division for the points on sphere, but I used only spatial division.

NSOL 2.x adopt a method by sorting algorithm.

1. Sort and index atoms by x-, y-, z-coordinates, respectively, using quick sort algorithm. When number of atoms less than 8, simple insertion method is used.
2. To an atom index i, the two farthest atom indexes si,n and li,n are obtained for each coordinates.
3. Neighbor atoms of an atom index i are obtained by logical operations and calculations of distances.
4. After making neighbor list, overlap checking is executed to each distributed points.

NSOL 3.x adopt my newest algorithm using mathematical morphology. In this method, distance calculation is not needed.

1. Make surface using mathematical morphology.
2. In each surface grids, mark distributed points on sphere and calculate surface area.

You can download each version of NSOL from following link:

^* Compare to nsol.f, nsol.c is slightly slower and does not have vector optimization code.

Usage: nsol [pdb file] [surface file]

Solvation Energy

Assuming that solvation energy is approximated in proportion to solvent accessible surface area.

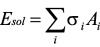
where σ_i: atomic solvation parameter,
A_i: solvent accessible surface area.

Several atomic solvation parameters have been proposed, such as, Ooi et al., Vila et al., Wesson et al., etc. And Temperature dependent solvation energy has been also proposed by Ooi et al.

References

oons: T. Ooi, M. Oobatake, G. Némethy, and H.A. Scheraga, Accessible surface areas as a measure of the thermodynamic parameters of hydration of peptides, Proc. Natl. Acad. Sci. USA (1987) vol.84, pp.3086-3090.

jrf_: J. Vila, R.L. Williams, M. Vásquez, and H.A. Scheraga, Empirical solvation models can be used to differentiate native from near-native conformations of bovine pancreatic trypsin inhibitor, PROTEINS: Structure, Function, and Genetics (1991) vol.10, pp.199-218.

we92, sch3: L. Wesson and D. Eisenberg, Atomic solvation parameters applied to molecular dynamics of proteins in solution, Protein Science (1992) vol.1, pp.227-235.

sch4: C.A. Schiffer, J.W. Caldwell, P.A. Kollman, and R.M. Stroud, Protein structure prediction with a combined solvation free energy-molecular mechanics force field, Molecular Simulation (1993) vol.10, pp.121-149.

Copyright © 1999-2010 Masato Masuya. All rights reserved.